Kodeknusere
Rømer var glad for hemmelige koder og kodeskrift. I denne kildepakke kommer du til selv at beskæftige dig med kodesprog og kryptering.
Rømer-kilden I skal arbejde med i denne kildepakke består af en række sider, hvor der står en masse tegn og ganske lidt tekst. Kilden er Rømers bud på, hvordan man kan lave et alfabet med symboler, som nemt kan huskes af den, der skal bruge det, men ikke kan afkodes af andre.
At Rømer har konstrueret et nyt symbolsk kodesprog kan måske virke lidt mærkeligt, og faktisk ved vi ikke præcist, hvorfor han gjorde det. Dog kan man forestille sig, at han måske har lavet det til brug i sit astronomiske arbejde og, at han er blevet sat til at lave kodesproget af kongen.
I forhold til, at han kunne bruge det til sit arbejde som astronom, så gav det dengang meget god mening at bruge et kodesprog, når du skulle observere himmellegemerne. Man skal forestille sig, at Rømer sad oppe i et observatorium (for eksempel Rundetårn) om natten og kiggede op på stjernehimlen, når det var mørkt (og ofte også koldt). Her har det været praktisk at have et kodesprog, så man hurtigt kunne notere observationer ned. Men mere sandsynligt er det imidlertid, at Rømer blev sat til at udarbejde kodesproget for kongen.
En allround videnskabsmand
At kongen bad Rømer om at lave et sprog, har dels noget med Rømers evner som matematiker at gøre og dels den politiske udvikling i samfundet. Rømer var officielt ansat som kongens “Hof matematikus” - kongens matematiker. Det betød ikke, at Rømer kun var ansat som matematiker, men en slags allround-videnskabsmand, som kunne svare på eller løse problemer af videnskabelig art.
Omkring 1700 var det blevet endnu vigtigere, at et samfund (eller en konge/regent) kunne skrive og læse hemmelige dokumenter også eksempelvis til og fra udlandet. I takt med at samfundet blev mere og mere kompleks, blev det også vigtigt for kongerne og regenterne rundt omkring i Europa, at man kunne spionere på hinanden for eksempel i forbindelse med krig og selv holde information hemmeligt. Her fik matematikken en væsentlig rolle at spille. Men før vi kigger nærmere på matematikkens rolle i forhold til at udvikle kodesprog på, er det vigtigt først at se på, hvordan matematikken udviklede sig i perioden omkring år 1700.
Matematik omkring år 1700
I løbet af 1600-tallet opstod den ‘moderne’ videnskab i takt med, at der dels kom mere fokus på de forskellige videnskabelige discipliner og dels på de videnskabelige metoder (se kildepakke 2).
Det nye ideal for videnskaben var, at man skulle observere og eksperimentere blandt andet ved hjælp af nogle af de nye videnskabelige instrumenter, som blev opfundet op gennem 1600-tallet, som for eksempel teleskopet og mikroskopet. Men udover den tekniske udvikling, så var det især matematikken som fik en ny rolle at spille.
Sagt lidt firkantet, så var det, som virkelig revolutionerede videnskaben og gjorde den moderne, at man gjorde matematikken til det videnskabelige sprog. Det vil sige, at matematikken blev en slags grunddisciplin og grundsprog for de andre naturvidenskabelige fag, og at matematikken blev den måde, hvorpå man kunne beskrive naturen og verden. Én af de matematikere, der især var vigtigt for denne udvikling, var franskmanden René Descartes (1596-1650), som fundamentalt ændrede den måde, man forstod og brugte matematikken på.
Siden antikken havde matematikken især handlet om at bevise ting. For grækerne havde matematik især med geometri at gøre og ikke mindst at bevise noget om geometriske former. Matematik var dermed et meget konkret redskab til at bevise nogle meget konkrete forhold, så hvis en græsk matematiker skulle bevise noget om en trekant, var han nødt til at tage udgangspunkt i trekanter.
I 1630erne indførte Descartes, at matematikken består af to elementer: de faste konstanter (som man kendte fra antikken), som han kaldte a, b, c, og de foranderlige variabler, som han kaldte x, y, z. Det betød, at nu kunne matematikerne oversætte spørgsmål, som handlede om trekanter til at handle om variabler i stedet. Og det betød, at man ikke længere var bundet af geometriske former og kunne løse ligninger på en ny måde.
Descartes påpeger dermed også, at matematik ikke er virkelighed, men et sprog som vi kan bruge til at vise noget om verden på. Eller sagt på en anden måde: Matematik er ikke virkeligheden, men matematisk sprog kan være en god beskrivelse af virkeligheden - og matematik kan også bruges til at analysere denne beskrivelse. Dette blev også vigtigt i udviklingen af kryptering på følgende måde: der findes en klartekst (virkeligheden), som vi oversætter til en krypteret tekst (matematisk beskrivelse), og vi kan bruge matematik til at analysere denne oversættelse (meta-matematik), og særligt til at undersøge måder at bryde krypteringen på.
Kodemestrene
Et kryptosystem (eller en cifferskrift) er en måde at sende hemmelige beskeder mellem en afsender (Alice) og en modtager (Bob), således at en udefrakommende (fjendtlig spion) ikke (umiddelbart) kan læse beskedens indhold.
Systemet er bygget op af to processer: I sin ende skal Alice tage en tekst og kryptere (eller indkode) den til en kryptotekst. Denne kryptotekst er så den, som hun sender til Bob. Bob skal tage kryptoteksten og afkode den til klartekst, der så — hvis ellers systemet virker — er identisk med den klartekst, Alice ville sende. Hemmeligheden i systemet ligger i, at Alice og Bob har en eller anden form for delt, hemmelig information om, hvordan klarteksten er krypteret og skal afkodes, og at det er svært (for spionen) at afkode kryptoteksten uden at kende til denne delte information.
Som nævnt tidligere, så var Rømer en ægte altmuligmand for kongen, og blandt de opgaver, han tog på sig, var at opfinde et cifferskrift, det vil sige en måde at skrive hemmelige meddelelser, så de ikke kunne brydes af fjendens spioner.
Den simpleste måde at gøre en tekst ulæselig på, var at bytte hvert bogstav ud med et andet tegn. Det kunne man eksempelvis gøre ved at rotere alfabetet et antal pladser — det kaldes Cæsar-koder — eller ved at skrive helt andre symboler for bogstaverne. Det sidste eksperimenterede Rømer med i sine noter, hvor han blandt andet benyttede følgende oversættelse: I kilden angiver Rømer, at koden er let at huske, for eksempel fordi tegnet for g, nemlig Λ, har form af en gavl, og tegnet 」er et omvendt L. Man kan også gøre teksten svær at læse ved for eksempel at fjerne nogle af bogstaverne (for eksempel alle vokaler og mellemrum) eller ved at trække kombinationer af bogstaver sammen til et enkelt tegn.
Rømer forsøgte jo at gøre sit alfabet og de enkelte tegn lette at huske. Men selv hvis vi ikke kender oversættelsen som i figur 1, kan vi faktisk godt bryde lignende koder.
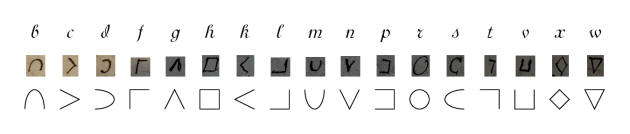
Foto: Det Kgl. Bibliotek
Hvis vi ved, at følgende kryptotekst er resultatet af en kryptering af en dansk tekst med en ren 1-1-udskiftning (substitution) af bogstaverne, men vi ikke kender måden, denne udskiftning virker på, så kan vi alligevel godt gøre forsøg på at bryde koden.
Lad os altså antage, at vi har opsnappet en kryptotekst skrevet med bogstaverne fra det komplette danske alfabet. Hvis vi ved, at dette er resultatet af en fast ombytning af bogstaverne i klarteksten, så kan vi ved at tælle forekomster få en god ide om i hvert fald visse dele af denne oversættelse ved at sammenholde frekvenser i kryptoteksten med frekvenser i det almindelige sprog (se figur 6).
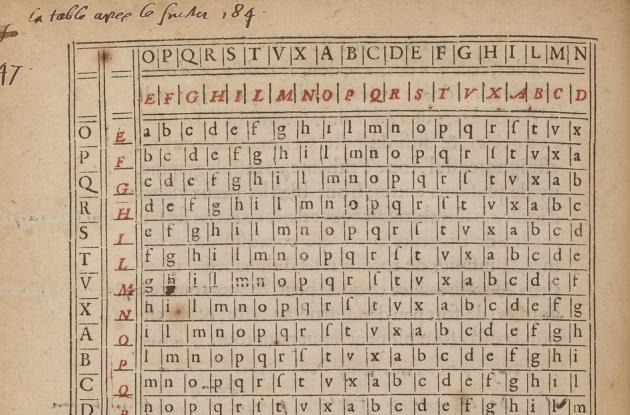
Allerede i 1500-tallet, altså længe før Rømer, havde andre matematikere imidlertid udviklet et andet kodesystem, som var mere kompliceret, men også mere sikkert, og det blev først brudt i 1800-tallet. Denne kode bliver i dag opkaldt efter Blaise de Vigenère (1523–1596), som beskrev den i sit værk "Traicté des ciffres,ou secretes manieres d’escrire" fra 1586. I sin bog angiver Vigenère flere forskellige kodesystemer, hvoraf det mest berømte er baseret på tabellen kaldet tabula recta:

Foto: Blaise de Vigenère
Vigenères kode er baseret på, at afsender og modtager foruden tabellen deler en nøgle, det vil sige en (kort) streng af bogstaver, som de er blevet enige om at bruge til at kryptere og afkode deres meddelelser.
Lad os forestille os, at de er blevet enige om nøglen SKOLE, og at afsenderen ønsker at sende klarteksten JEG KAN GODT LIDE IS. Når vi fjerner mellemrum i klarteksten, er den 16 tegn lang, og fordi Vigenères tabel ikke indeholder J, K og U, erstatter vi disse bogstaver med I, C og V (i denne klartekst er der jo ikke brug for at erstatte U, da det ikke forekommer). Så er vi klar til at kryptere beskeden, og det gør man ved først at gentage nøglen ovenover klarteksten som vist i figur 2:

Foto: Det Kgl. Bibliotek
Til krypteringen skal vi nu bruge denne tabula recta, og vi skal her se bort fra de bogstaver, der er skrevet med rødt. Vi begynder med det første bogstav i klarteksten, som er I (blå cirkel) og det bogstav, der står over det, nemlig S (rød cirkel). Så finder vi den søjle i tabellen, der står under I, og den række i tabellen, der står ud for S. Det bogstav, der står i den celle, der deles af denne søjle og række, her a, er det krypterede tegn. Således gøres for hvert bogstav i klarteksten, der hver for sig krypteres med et skiftende bogstav fra nøglen. Processen og dens resultat er illustreret i figur 2.
Når man skal afkode en besked skrevet med Vigninère-kode, skal man igen bruge den delte nøgle og tabula recta, men i omvendt rækkefølge. Hvis for eksempel nøglens første bogstav er S, og kryptotekstens første tegn er a, så skal man finde den række, der hører til S, og deri finde forekomsten af a. Det bogstav, der står øverst i søjlen med a, her I, er det tilhørende bogstav i klarteksten.
Opgave 1
- Afkod beskeden i denne kode:
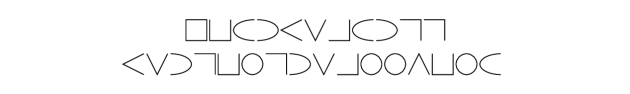
Foto: Det Kgl. Bibliotek
- Tæl op, hvor mange gange de forskellige bogstaver forekommer i klarteksten, og hvor mange gange de forskellige tegn forekommer i den krypterede tekst. Er der nogen sammenhæng, hvordan/hvordan ikke?
- Lav en kodet besked med Rømers kode og giv den til en af dine kammerater at afkode?
- Hvad skal afsender og modtager dele af hemmelig information, for at afkodningen virker?
- Diskuter kort, hvor sikker de hemmelige informationer og om der nogen mulighed for at de bliver misforstået?
Opgave 2
- Afkod beskeden i figur 5, ved at bruge nøglen SKOLE

Foto: Det Kgl. Bibliotek
- Tæl op, hvor mange gange de forskellige bogstaver forekommer i klarteksten, og hvor mange gange de forskellige tegn forekommer i den krypterede tekst. Er der nogen sammenhæng? Hvordan/hvordan ikke?
- Vælg en nøgle og skriv en kodet besked med Vigenères kode og giv den til en af dine kammerater at afkode.
- Hvad skal afsender og modtager dele af hemmelig information, for at afkodningen virker?
- Diskuter kort, hvor sikker denne hemmelige information er?
Opgave 3
- Sammenlign hvor svære og tidskrævende de to kryptosystemer (Rømers og Vigenères) er at bruge til indkodning og afkodning. Hvilke redskaber kan/skal man have? Hvad sker der, hvis de falder i spionens hænder?
- Hvis vi nu har opsnappet kryptoteksten i figur 7 og har god grund til at tro, at klarteksten er skrevet på dansk, så kan vi forsøge at afkode den ved at tælle forekomster af bogstaver og sammenligne med et korpus af dansk tekst (se for eksempel figur 6). Hvor langt kan du komme med at bryde koden i figur 7?
- Virker den form for statistisk analyse på Vigenère-kryptosystemet?
- Hvordan kunne du modificere Rømers kode, så den blev sværere at bryde
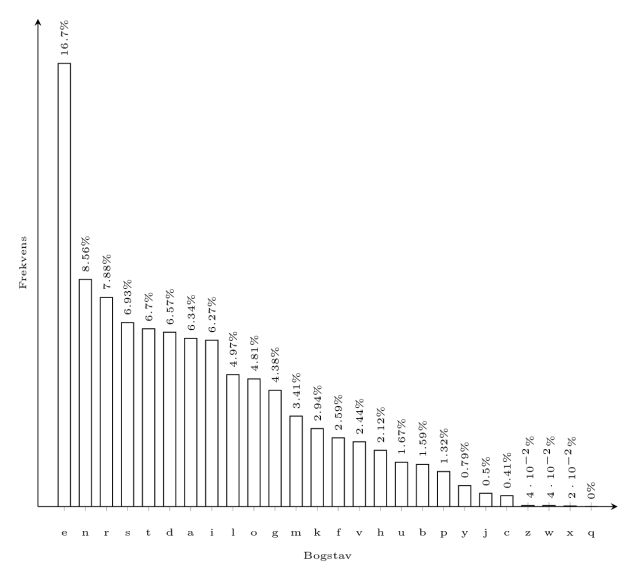
Foto: Det Kgl. Bibliotek

Foto: Det Kgl. Bibliotek
Opgave 4
Når man skal ind- og afkode en besked ved hjælp af Vigenère-systemet, skal man hele tiden slå op i tabula recta. Men man kan også forsøge at gøre det smartere ved hjælp af en kryptoskive (et Vigenère-hjul) som vist i figur 8.
Når du vil indkode eksempelvis klartekstbogstavet E med nøglebogstavet T, så skal du rotere skiverne, så A på den ydre skive står over T på den indre. Så skal du finde E på den ydre skive; det står ud for X på den indre skrive, og så er X det søgte kryptobogstav.
- Kryptoskiven i Figur 8 er beregnet til engelsk tekst. Konstruér en kryptoskive af papir eller pap med alle de sædvanlige danske bogstaver. Klip det ud og saml det.
- Kan du bruge det til at skrive og afkode hemmelige beskeder?
- Søg eventuelt flere informationer om kryptoskiver (engelsk.: ’cipher discs’) på nettet og dekorér din kryptoskive ud fra, hvad du finder.
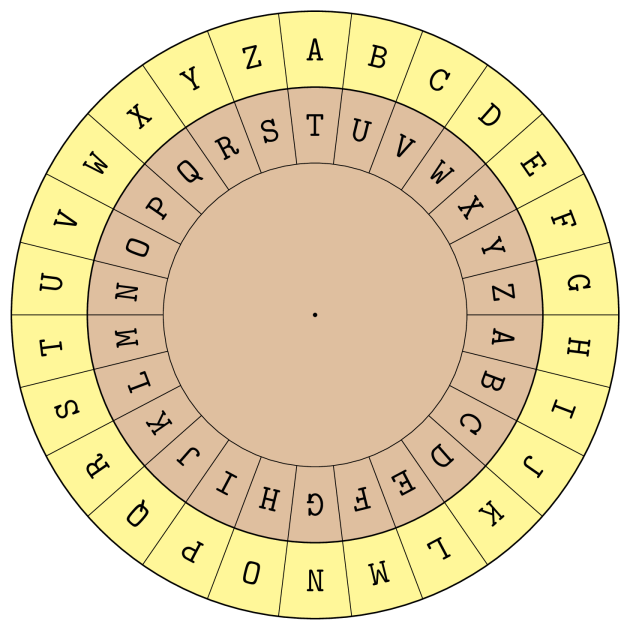
Foto: Det Kgl. Bibliotek
Kilder
- Ole Rømer “Om et alphabet med characterer at skrive med so kand ihukommis och af ingen dissifreris” i Additamenta 265 b 4to (side 11).
- Vigenère, Blaise de. Traicté des ciffres, ou secretes manieres d’escrire fra 1586.