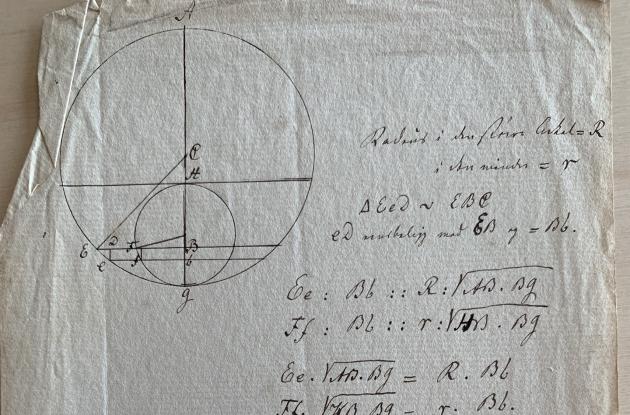Lærebog og penduler

I kildepakken skal I beskæftige jer med penduler og bevægelseslære og blandt andet kigge på nogle af Ørsteds noter fra hans lærebog om mekanisk fysik.

Baggrund

Folio 5 i Ørsted-arkivet hedder ”Optegnelser vedkommende Lærebogen” og består både af tegninger og notater. Lærebogen, der her omtales, er Ørsteds lærebog i mekanisk fysik, som var et projekt, som Ørsted arbejdede på, hvor han ville skrive en ”Bevægelseslære”. Den anden kilde i denne kildepakke er fra det omslag, Ørsted havde rundt om sit manuskript til ”Forelæsning over Naturvidenskabens Aand”. Udregningen på omslaget står helt nede i hjørnet, og man kan undre sig over, hvorfor det står der. Kigger man på bagsiden af omslaget, ser man, at han har noteret kort om nogle hollandske ord. Måske har omslaget lige været ved hånden, da Ørsted skulle lave udregningen eller notere om det hollandske sprog og fungerede som et notepapir for ham?

I forlængelse af opgaverne finder du en uddybende forklaring på Ørsteds argument.

Manuskriptsiden med Ørsteds figur og udregninger uden yderligere meget forklaring. Indholdet handler om pendulbevægelser.
Foto: Det Kgl. Bibliotek

Detalje fra et af Ørsteds manuskripter, hvor man kan se, at han benytter Leibniz-notationen dx og dy til at opstille differentialligning. Foto: Det Kgl. Bibliotek
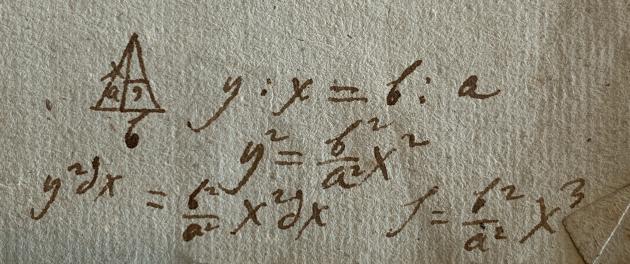
Foto: Det Kgl. Bibliotek

Kildemateriale

Kildeside fra folio 5 samt forsiden på omslaget til folio 6 fra Ørsted-arkivet (links på vej, se i de to illustrationer ovenfor).

Opgave 1

Konstruer Ørsteds figur fra folio 5 (enten i hånden eller i et geometri-program):

Forklar hvordan de forskellige dele af konstruktionen afhænger af hinanden (her får du brug for at kigge på Ørsteds argument).

Opgave 2

Følg og forklar Ørsteds argumentation. Vær særlig opmærksom på følgende sværere, men centrale punkter:

Hvad betyder „△EeD ~ EBC“ mon, og hvordan indser man at det gælder? Hvilke antagelser er du nødt til at gøre undervejs?
Diskuter, hvad det mon er, Ørsted skriver om relationen mellem eD og EB, og hvordan man ud fra sammenhængen kan finde ud af det?
Undervejs argumenterer han ud fra forholdene i en trekant på en cirkels diameter. Find og forklar et bevis for resultatet i figur b (nedenfor). Det kan enten være et klassisk geometrisk bevis fra Euklids "Elementer" (se for eksempel Euklid II.5), et bevis ved at oversætte til algebraisk notation, et eksperiment, et trigonometrisk bevis eller noget helt femte.

Opgave 3

Kig igen på kilden fra folio 5 om lærebogen, som Ørsted planlagde skulle indgå som del af en lærebog om bevægelseslæren:

Hvilken fysisk situation, er det mon Ørsted er i gang med at modellere i kilden?
Hvordan vil du karakterisere hans brug af matematisk notation og fysisk argumentation?
Kig op kilden fra folio 6 (omslaget): Denne udregning er fundet et helt andet sted i arkivet - har det noget med den anden udregning at gøre? Sammenlign hans notationer og argument.

Forklaring

Ørsteds argument begynder med, at han noterer, at trekanterne EeD og EBC er kongruente (se figur a). Denne konklusion afslører, at han stiltiende antager, at e ligger på den store cirkels tangent i E, idet han da vil have, at vinklen ∠CEe er ret, og dermed ∠CEB + ∠DEe = 90˚.

Dernæst betragter Ørsted forhold i de ensvinklede trekanter, som opfatter som trekanter på en cirkels diameter (se figur b). Da trekanterne EeD og EBC er ensvinklede, er Ee ∶ eD = EC ∶ eB; og da eD = bB, EC = R og EB ² = AB · Bg, følger det første forhold. Det andet forhold følger tilsvarende for den lille cirkel, og derefter ganger Ørsted over kors og samler led til relationen

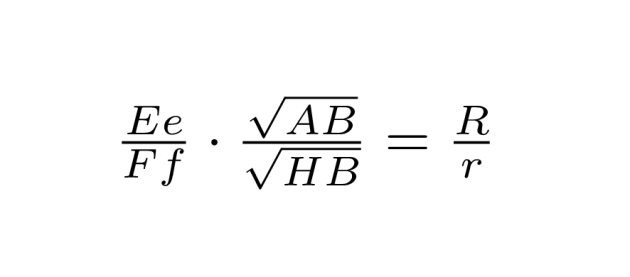
Formel der udtrykker forholdet mellem de to radier R og r ved hjælp af de indgående størrelser.
Foto: Det Kgl. Bibliotek

Nu kommer en del af kilden, som ser (endnu mere) mærkelig ud med moderne øjne. Ørsted indfører tilsyneladende en længde g, selvom dette symbol også henviser til et punkt på figuren. Dernæst hævder han, at AB = 2R, når Bg er (uendeligt?) lille, hvorfra han udleder

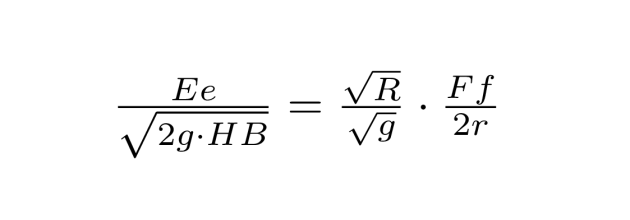
Formel der udtrykker relationer i Ørsteds figur. — Formel udledt af ovenstående, der udtrykker relationer i Ørsteds figur.
Foto: Det Kgl. Bibliotek

Denne udledning er syntaktisk korrekt givet antagelserne, men for at se konteksten er vi nødt til at se på, hvad det er for en fysisk situation, Ørsted er i gang med at analysere. Vi får et hint i den allersidste formel, som angiver svingningstiden som

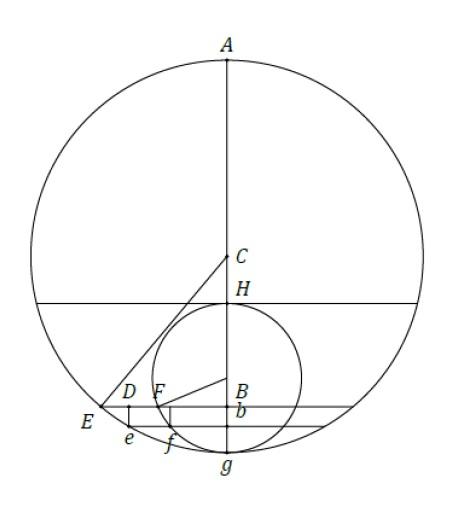
Matematisk figur gentegnet ud fra Ørsteds figur med anvisninger — Figur a: Gentegning af Ørsteds figur.
Foto: Det Kgl. Bibliotek

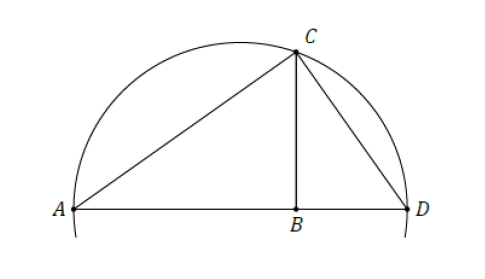
Figur der illustrerer en trekant konstrueret på diameteren i en cirkel — Figur b: I en trekant på en diameter er BC² = AB · BD.
Foto: Det Kgl. Bibliotek