Ørsteds æstetiske ellipser
I denne kildepakke skal I se på Ørsteds matematiske beregninger af ellipser og nogle af hans originale håndtegnede ellipser.
Baggrund
Ørsted er primært kendt for sit videnskabelige arbejde med fysik og kemi, men enkelte af hans værker omhandler geometri. Geometrien spiller en væsentlig rolle i hans værker om æstetikken (det skjønnes Naturlære, som han betegner det), hvor han blandt andet kommer ind på symmetriens rolle i forhold til æstetikken (se også kildepakke 2).
Kildemateriale
- Uddrag fra ”Dialog om Symmetrien” fra Folio 47 (s. 99-100)
- Uddrag fra Ørsteds ”Samlede og efterladte Skrifter” (1851-2) bind 3 (uddrag)
Opgave 1
Kig på de to tegninger, som er sat ind i margin på kilden. Læs herefter s. 134-139 (fra: Herman: Du synes saaledes at Symmetrien
til: Herman: Jeg giver Dig gjerne Ret i alt dette
)
Introduktion til teksten
Ørsteds manuskript om symmetrien er skrevet som en dialog mellem vennerne Alfred og Herman, der diskuterer, hvad principperne for æstetikken er (det vil sige, hvad det skønnes naturlære er). I den anden halvdel af den tredje dialog, som generelt omhandler symmetrier, drejer samtalen sig ind på matematikkens figurer og former. I dialogen lader Ørsted hovedpersonen Alfred fremsætte flere pointer omkring et dynamisk geometrisyn: Den blotte Figur staaer sjeldent ene; den frembringes tit ved Virksomheder, som gjore Skjønheden rigere
(s. 134).
Dette eksemplificerer Alfred med de ”Bølgekredse”, som frembringes, når man kaster en sten i vandet. Heraf udleder Alfred: Det er ikke Kredsene, som her danne Udgangspunktet, men Bevægelsen. Denne danner Kredse, kredsformige Bølgebjerge og Bølgedale; de ere nødvendige Følger af Bevarelseslovene; men de kunne ikke opfattes af Øiet uden Lyset, og saa sandt som de skulle sees, maae de fremtræde i deres Lysforhold med Glands, med Lys og Skygge og med det Lysspil, Bevægelsen giver
(s. 135).
Til dette har han brug for en figur af en ellipse, og i manuskriptet har Ørsted tegnet sit forlæg til den udgivne version i margin. Men figuren i manuskriptet er ikke helt præcist en ellipse (se opgave 3).
- Hvordan kan du afgøre, om Ørsteds håndtegnede figur er en ellipse eller ej?
Opgave 2
- Hvordan tror du, at Ørsted kan have tegnet sin ellipse og de tilhørende tangenter?
- Hvordan tror du, at den udgivne figur er blevet til?
- Hvad siger dine observationer dig om den rolle, som figurer spillede i matematiske argumenter i 1800-tallet? Og i dag?
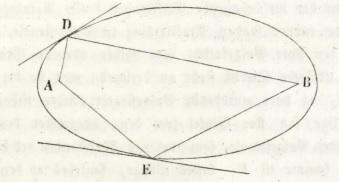
Foto: Det Kgl. Bibliotek
Foto: Det Kgl. Bibliotek
I arbejdet med at svare på opgave 2 får du brug for at gå undersøgende til værks og nærmest betragte opgaven som en detektivopgave, hvor vi er givet forholdsvist få spor. Men så må man studere dem i detaljer eller søge informationer andre steder, for eksempel ved at bruge søge information på nettet.
Et af de hints, vi er givet, er de indtegnede linjer AE og EB (og tilsvarende med D). Måske kan de medvirke til at svare på opgaven, hvis man kan finde ud af, hvad der karakteriserer en ellipse? Som forklaring fremdrager Alfred en karakteristik af ellipsen:
”Ellipsen har, som bekjendt, to Hovedpunkter, som man kalder Brændpunkter, og som have en saadan Stilling, at to Linier, dragne fra et Punkt i Omkredsen hen til dem, gjøre ligestore Vinkler med den Tangent, der lader sig drage til dette Punkt”. (s. 137)
”A og B ere Brændpunkterne. AD og BD ere to Linier, som vi her uden at holde os til Kunstsproget ville kalde Straalelinier; ved D seer Du en ret Linie, som danner lige Vinkler med begge og falder sammen med den uendeligt lille Deel af Buen, som den berører. I Skæringspunktet af AE og BE seer Du det samme. Hvert Par sammenhørende Straalelinier udgjøre altid, naar de lægges sammen, en lige Sum”. (s. 137)
Opgave 3
- Kan du (med dine egne ord, begreber og symboler) forklare Ørsteds karakteristik af ellipsen ovenfor? Hvilken opfattelse af ellipsen lægger du til grund for din udledning og forklaring?
- Kan du (med dine egne ord, begreber og eventuelt symboler) forklare Ørsteds beskrivelse af tangentens egenskaber ovenfor?
- Kan du (med dine egne ord, begreber og symboler) formulere og bevise den sætning, som Ørsted fremsætter i slutningen af citatet ovenfor?
Foto: Det Kgl. Bibliotek
Figuren ovenfor viser, at Ørsteds håndtegning er meget tæt på, men ikke helt præcist en ellipse.
Opgave 4
Læs nu §7 og §12 “Om Symmetrien og de ved den frembragte Skjønhedsundtryk”: Ørsteds tekst fortsætter med en spændende diskussion af bølgerne i et ellipseformet kar Læs nu §1§7, §12 fra ”Bidrag til det Skjønnes Naturlære” (s. 155) og svar på følgende:
- Hvordan er cirklen ultimativ i sin symmetri (§7)? Hans ’bevis’ er i § 12 om, hvordan 3 ikke er æstetisk behageligt for øjet, men 8 er.